
Электронный учебник по физике 10 класса
по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.
![]()
|
|
Электронный учебник по физике 10 класса по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.
|
|
|
Страничка интересных физических явлений и событий | ||||||||||
| Бегемот и птичка Представь, что тебе понадобилось приподнять шкаф. Не хватает сил? Не горюй! Подсунь под край шкафа крепкую палку — и ты приподнимешь его без особого труда. Ты хочешь раздавить орех и не можешь сделать это руками. Ну что же. Есть специальные щипцы для орехов. С их помощью ты легко справишься с этой задачей. Тебе нужно разрезать жесть. Ты, конечно, не станешь делать это ножом. Нет, ты возьмешь ножницы по металлу. Хорошие ножницы режут жесть, как бумагу. Все эти случаи на первый взгляд очень разные. И все-таки они похожи один на другой. У тебя не хватило силы, чтобы сделать ту или иную работу. Тогда ты берешь в руки какое-то приспособление — и работа сразу становится тебе по силам! И самое удивительное здесь то, что приспособление — палка, щипцы, ножницы — не имеет двигателя, не имеет никакой собственной силы. Оно только увеличивает ту силу, которую прикладываешь ты. Чтобы понять, как это получается, проделай опыт. Возьми два предмета разного веса. Я брал фарфоровую фигурку бегемота и гораздо более легкую деревянную птичку. Посади их на концы линейки, положенной серединой на круглый карандаш. Кто перетянет? Ясно, что бегемот. Он ведь тяжелее. Ну а если сдвинуть карандаш поближе к бегемоту? Еще, еще ближе! Смотри-ка: птичка и бегемот уравновесились! А подвинь карандаш еще ближе к бегемоту — и птичка перевесит! Что же понадобилось легкой птичке для того, чтобы перетянуть тяжелого бегемота? Приспособление, состоящее из линейки и карандаша. Линейка опирается на карандаш. Место, в котором она опирается, называют точкой опоры. В этом опыте мы взяли линейку потому, что на нее удобно ставить фигурки. Можно было бы взять и круглую палку, и брусок, да и мало ли какой еще продолговатый предмет. Действие было бы тем же самым, только птичку и бегемота пришлось бы не ставить, а привязывать, или подвешивать, или приколачивать. Длинную палку с точкой опоры называют рычагом. Это очень древнее приспособление. О рычаге сказал великий механик и математик древности Архимед из Сиракуз: «Дайте мне точку опоры — и я сдвину Землю!» Палка, подсунутая под шкаф,— это рычаг. И ты своим «птичьим» нажимом поднимаешь на ней «бегемота» — целый шкаф. Каждая половинка щипцов для орехов — это рычаг. Поэтому «птичка» —твои пальцы — осиливает «бегемота» — сопротивление твердого ореха. И каждая половинка ножниц — тоже рычаг. Поэтому «птичка» — твоя рука — и на этот раз осиливает сопротивление толстой жести. Птичкина хитрость |
|
||||||||||
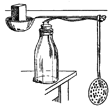
| Рычажные весы Вспомни, как тебя взвешивали при врачебном осмотре. Стоя на платформе весов, ты играл роль бегемота из нашего предыдущего опыта. А роль птички исполняла гиря, которую передвигала по коромыслу весов медицинская сестра. Конечно, эти весы устроены сложнее, чем в нашем опыте. В них спрятаны два рычага, расположенные один за другим. Но основной принцип тот же самый. Гиря по коромыслу передвигалась далеко, а движение платформы весов было едва-едва заметным. Очень похожи по устройству и большие товарные, так называемые десятичные, весы. Их можно увидеть на товарных складах и в багажных отделениях станций железной дороги. На почте взвешивают посылки тоже на рычажных весах. Хозяйственные, кухонные весы чаще выпускают пружинными, со стрелкой и циферблатом. Но иногда в кухне можно увидеть и рычажные весы. Ты тоже можешь сделать кухонные рычажные весы. Рычагом, да заодно уже и чашкой этих весов, будет служить поварешка, подвижной гирей — шумовка, точкой опоры для рычага тут будут зубья вилки. Они лежат на шляпках двух гвоздей, воткнутых в пробку. Другой конец вилки вставлен в крючок поварешки вместе с кусочком пробки, чтобы не выпадал. На стене проведи горизонтальную линию. Как это сделать — объяснено в главке «Как повесить картину?». Взвешивая груз, передвигай шумовку до тех пор, пока поварешка не установится параллельно этой линии. На коромысле почтовых и медицинских весов нанесены деления. И на ручке поварешки их тоже нужно будет нанести. Сперва отметь положение шумовки на поварешке без груза. Потом положи в черпак поварешки груз в 0,5 кг и передвигай шумовку, пока снова не установишь равновесие. Отметь и это положение шумовки. Промежуток между двумя отметками раздели по линейке на пять равных частей и проставь около делений цифры: 0; 0,1 кг; 0,2 кг, и так до 0,5 кг. Весы готовы! |
 |
||||||||||
| Послушное и непослушное яйцо Проткни в концах яйца две дырочки величиной со спичечную головку и выдуй содержимое. Внутренность яйца промой несколько раз водой. Чтобы скорлупа хорошенько просохла изнутри, дай ей полежать один-два дня. После этого одну дырочку залепи гипсом, клеем с мелом или с белилами так, чтобы она не была заметна. Насыпь в скорлупу чистого и сухого песку примерно на четверть. Залепи вторую дырочку таким же образом, как первую. Послушное яйцо готово! Ты сможешь поставить его в любом положении. Для этого нужно только слегка встряхнуть яйцо, держа его в том положении, которое оно должно будет занять. Песчинки переместятся, и поставленное яйцо будет сохранять устойчивое равновесие. Чтобы сделать непослушное яйцо, нужно вместо песка набросать в него 30-40 штук самых мелких дробинок («бекасинника») и кусочки стеарина от свечи. Потом поставь яйцо на один конец и подогрей. Стеарин растопится, а когда застынет, слепит дробинки между собой и приклеит к скорлупе. Замаскируй дырочки в скорлупе. Непослушное яйцо невозможно будет уложить. Оно будет стоять не только на столе, но и на краю стакана, на ручке ножа, на горлышке бутылки. Впрочем, такая игрушка тебе уже знакома. Это ведь ванька-встанька! Можешь сделать его по всем правилам. Для этого груз укрепи в тупом конце яйца, а скорлупу разрисуй и раскрась. Можешь даже приклеить ваньке бумажные ручки и сшить кафтанчик. |
|||||||||||
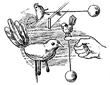
| Воробей на ветке Это простая и интересная игрушка с устойчивым равновесием. Тело и голову воробья вылепи из пластилина. Прекрасный клюв получится из шипа акации, терна или другого колючего растения. Если подходящего шипа нет, можешь просто заострить палочку и вдавить ее в пластилин. Глаза воробья — шляпки гвоздей, бусины или спичечные головки. Вместо хвоста воткни несколько перышек. Ноги — из спичек. На нижнем конце проволоки, воткнутой в тело воробья, укрепи противовес. Это может быть шарик из пластилина, небольшая картофелина, наконец, просто гайка, повешенная на крючок. В тело воробья проволока должна входить позади лапок. При достаточно тяжелом грузе воробей будет отлично сидеть на пальце. А если посадить его на ветку в саду, он будет покачиваться, как живой. Можно сажать его и на новогоднюю елку. Ну а что будет, если груз легче воробья? Усидит наша птичка или свалится? Когда мы ставили карандаш на острие, то выяснили, что равновесие будет устойчиво, если главная тяжесть находится ниже точки опоры. Теперь главная тяжесть — туловище воробья — выше точки опоры. Значит, бедняга упадет? Не торопись с ответом. Проверь сначала на опыте. Передвигай картофелину или пластилиновый шарик вверх и вниз по проволоке. Пытаясь уравновесить воробья при разных положениях легкого груза, ты увидишь, что птичка сидит устойчиво, когда груз сдвинут далеко вниз. А если груз высоко, под самым пальцем, то воробей будет опрокидываться. Выходит, что устойчивость равновесия зависит не только от веса, но и от положения груза. Чтобы получше в этом разобраться, можешь сделать еще один опыт с пластилиновым воробьем. Попробуй уравновесить его, подперев проволоку ребром линейки. Ты увидишь, что чем выше поднят противовес, тем ближе воробью то место проволоки, на котором она уравновешивается. Это место называют центром тяжести всего сооружения. Если не пожалеешь времени на пробы, ты увидишь, что воробей сидит на пальце до тех пор, пока центр тяжести остается ниже точки опоры. А как только он станет выше, воробей начнет падать. Значит, не обязательно, чтобы главная тяжесть была внизу. Важно, чтобы ниже точки опоры был центр тяжести. Тогда при нарушении равновесия центр тяжести будет подниматься. А поднять центр тяжести — это все равно что поднять весь груз вместе: и воробья, и противовес, и проволоку. Конечно, центр тяжести будет всегда тянуть вниз и равновесие будет восстанавливаться. |
 |
||||||||||
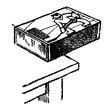
| Коробок с сюрпризом Казалось бы, с центром тяжести все стало ясно. Но тебя ожидает еще один сюрприз, и не маленький, хоть он и спрятан в спичечном коробке. Положи в этот коробок тяжелую гайку. Сдвинь ее как можно ближе к одному краю. Теперь этот край будет удерживаться на столе, даже если почти весь коробок висит в воздухе. Этот опыт далеко не так красив, как опыт с воробьем. Но есть в нем одна замечательная особенность. Здесь вся тяжесть лежит выше точки опоры, а коробок не падает. Почему? Теперь ты, наверное, сможешь догадаться. Дело в том, что, если коробок начнет переваливаться через край стола, гайка поднимется. Иными словами, при нарушении равновесия центр тяжести будет подниматься. Поэтому равновесие будет восстанавливаться. Интересно, что по этой же самой причине в устойчивом равновесии находятся столы, шкафы, кровати, памятники, автобусы, подъемные краны, садовые скамейки, тепловозы, галоши, стоящие под вешалкой, и еще тысячи самых разнообразных предметов, перечисление которых не поместилось бы в этой книжке! Общее свойство у них одно: при нарушении равновесия центр тяжести поднимается. Поэтому-то все они лежат, стоят, едут, не опрокидываясь. |
 |
||||||||||
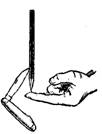
| А карандаш-то не падает! Попробуй поставить карандаш на острие. Вряд ли у тебя этот опыт получится. Можешь возиться хоть целый день! И все-таки есть очень простой способ заставить карандаш стоять. Всади в него перочинный нож, раскрытый не до конца! На рисунке ясно видно, как это сделать. Раскрывая нож больше или меньше, можешь устанавливать карандаш не только прямо, но и наклонно. И все равно он не будет падать, далее если его толкнуть. Немножко покачается — и останется стоять на острие! Почему же карандаш без ножа падает, а с ножом стоит? Ведь в обоих случаях карандаш опирается на острие. Это его точка опоры. Но в первом случае точка опоры находилась в самом низу. А во втором — под ней висел перочинный нож. Ясно, что дело здесь именно в ноже. Если карандаш наклонится и начнет падать — нож будет подниматься вверх. Но ведь нож тяжелее, он тянет вниз и заставляет карандаш снова выпрямиться. Значит, равновесие будет устойчиво, если главная тяжесть находится ниже точки опоры. |
 |
||||||||||
| Парадоксы и софизмы (софизм означает рассуждение, формально кажущееся совершенно безупречным, но содержащее на самом деле ошибку, в результате чего конечный вывод оказывается абсурдным. Например: "То, что ты не терял, ты имеешь; ты не терял рогов, следовательно, ты их имеешь". В парадоксе, наоборот, умозаключение, кажущееся неверным, противоречащим "здравому смыслу", на самом деле справедливо). | |||||||||||
| 1. УДИВИТЕЛЬНЫЕ ПРИКЛЮЧЕНИЯ ПАССАЖИРА
МЕТРО. Один из жителей Москвы каждое утро отправлялся на работу поездом метро. Хотя рабочий день у него начинался ежедневно в одни и те же часы, время его прихода на станцию могло, разумеется, несколько различаться в разные дни. Для простоты можно считать время прихода совершенно случайным. На первый взгляд кажется правдоподобным предположить, что число дней, когда после его прихода на станцию вначале появится поезд нужного пассажиру направления, будет примерно равно числу дней, когда первым прибудет поезд, идущий в противоположную сторону. Каково же было изумление пассажира, когда он обнаружил, что нужные ему поезда приходят на станцию в 2 раза реже, чем встречные! Решив выяснить причины непонятного явления, он стал отправляться на работу с другой станции, расположенной несколько дальше от его дома. Наблюдения, произведенные здесь, заставили его удивиться еще больше, так как на этой станции дело обстояло совершенно иначе: нужные поезда приходили первыми в 3 раза чаще! Помогите пассажиру разобраться в причинах столь странного поведения поездов метро. 2. БУДУТ ЛИ ДВИГАТЬСЯ АЭРОСАНИ? Предположим, что на конвейерной ленте установлена модель аэросаней, приводимая в движение воздушным винтом толкающего типа. Какова будет скорость модели относительно Земли, если конвейер и сани одновременно придут в движение в противоположных направлениях, т. е. будут ли сани оставаться на месте или двигаться в какую-либо сторону? |
|||||||||||
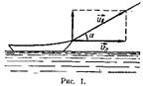
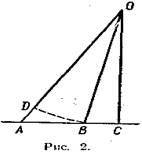
| 3. КАКОВА СКОРОСТЬ ЛОДКИ? Стоящий на берегу человек подтягивает к себе лодку, выбирая веревку, привязанную к носу лодки, с некоторой постоянной скоростью Uв. Разложим скорость Uв так, как показано на рисунке 1, Тогда для скорости лодки Vл получим: |Vл|=|Uв|cosa Из этой формулы следует, что, чем больше угол а, т. е. чем ближе лодка к берегу, тем меньше ее скорость. На самом же деле наоборот: по мере приближения лодки к берегу ее скорость должна возрастать, в чем легко убедиться на опыте. Достаточно привязать к карандашу нитку и потянуть за нее так, как тянули лодку. Доказать, что полученное выражение не согласуется с опытом, можно также графически (рис. 2). Пусть за некоторый интервал времени t нос лодки перемещается из точки А в точку В, пройдя при этом расстояние АВ. Если АО — первоначальное положение веревки, а ВО — ее положение к концу интервала t, то, отложив на АО отрезок OD, равный ОВ, мы найдем, на сколько нужно вытянуть веревку (отрезок AD), чтобы лодка прошла путь АВ. Из чертежа хорошо видно, что AB>AD. Следовательно, |V|>|U|, что противоречит формуле |V |=|U |cos a, так как косинус угла всегда меньше единицы. В чем же причина расхождений теории и опыта? |
 |
||||||||||
 |
|||||||||||
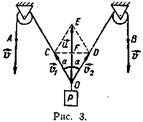
| 4. СТРАННЫЙ РЕЗУЛЬТАТ СЛОЖЕНИЯ СКОРОСТЕЙ. Рабочие поднимают груз Р с помощью привязанных к нему веревок, перекинутых через два неподвижных блока (рис. 3). Рассчитаем скорость груза в тот момент, когда веревки образуют между собой угол 2а, если рабочие выбирают концы A и В веревок с равными по модулю скоростями |V1| = |V2|=|V|. Руководствуясь правилом параллелограмма, находим для модуля скорости |U| груза | U| =2 ОЕ=2 ОС cos a=2 |V | cos а. Проанализируем полученный результат. Пусть груз находится не очень высоко, а блоки не слишком удалены друг от друга. Тогда угол а близок к 0°, так что его косинус с большой степенью точности можно положить равным единице и приведенная выше формула дает: |U|≈2|V|. Нелепость выражения очевидна: груз не может подниматься со скоростью, превышающей скорость вытягивания веревки! Значит, наши рассуждения содержат ошибку. В чем же она заключается? |
 |
||||||||||
| 5. ЧЕМУ РАВНА СРЕДНЯЯ СКОРОСТЬ? Из пункта А в пункт В мотоциклист двигался со скоростью 60 км/ч; обратный путь им был проделан со скоростью 40 км/ч. Определите среднюю скорость мотоциклиста за все время движения, пренебрегая лишь временем остановки в пункте В 6. ТИШЕ ЕДЕШЬ — СКОРЕЕ ПРИЕДЕШЬ! Пусть необходимо определить начальную скорость брошенного вертикально вверх камня, оказавшегося спустя 4 с после броска на высоте 6 м. Разрешим уравнение перемещения прямолинейного равнопеременного движения относительно начальной скорости V0=(2S-at2)/2t и вычислим полученное выражение при заданных выше условиях, полагая ускорение свободного падения равным для простоты -10 м/с2 (знак минус означает, что ускорение направлено в сторону, противоположную отсчитываемому перемещению): V0=(2*6м+10м/с2*16с2)/(2*4с)=21,5м/с Как должна измениться начальная скорость, чтобы на той же высоте (6 м) камень оказался через вдвое меньшее время? Необходимость ее увеличения кажется совершенно очевидной. Однако не будем спешить! Предположив, что на высоте 6 м камень будет не через 4 с, а через 2 с, получим: V0=(2*6м+10м/с2*4с2)/(2*2с)=13м/с Вот уж воистину как в поговорке: «Тише едешь-дальше будешь!» 7. «ВОПРЕКИ» ЗАКОНУ ИНЕРЦИИ. Первый закон механики может быть сформулирован следующим образом: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не заставит его изменить это состояние. Почему же в таком случае мы часто наблюдаем, как пассажиры, стоящие в вагоне подходящей к станции электрички, наклоняются в момент остановки не вперед, как того требует закон инерции, а в противоположную сторону? 8. ВЕС ТЕПЛОВОЗА РАВЕН ВЕСУ ВАГОНОВ. Если бы трение между ведущими колесами тепловоза и рельсами отсутствовало, то тепловоз не был бы в состоянии сдвинуть поезд с места. Согласно третьему закону Ньютона сила тяги, развиваемая при равномерном движении, в точности равна силе трения между его ведущими колесами и рельсами: Fтяги=Fтр=k1P1 где k1 — коэффициент трения колес тепловоза, которые мы все считаем для простоты ведущими, о рельсы; Р — вес тепловоза. Также на основании третьего закона Ньютона сила тяги должна быть равна той силе, против которой локомотив производит работу, т. е. при равномерном движении равна силе трения колес вагонов о рельсы: (Р2 — вес вагонов). Сравнивая эти выражения, находим: k1P1=k2P2 Сокращая на k1=k2 (трение стали о сталь), получим явную нелепость: P1=P2 т. е. вес тепловоза равен весу вагонов?! |
|||||||||||
| 9. ПОЧЕМУ КОНЦЫ ОСЕЙ, ЛЕЖАЩИЕ В ОПОРНЫХ
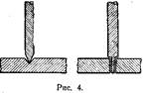
ПОДШИПНИКАХ, ЗАТАЧИВАЮТ «НА КОНУС»? Сила трения, как известно, определяется только коэффициентом трения, зависящим от рода соприкасающихся поверхностей, и силой нормального давления, но практически не зависит от площади трущихся поверхностей. Почему же в таком случае концы осей, лежащие в опорных подшипниках, затачивают «на конус», а концы осей, закрепленные в подшипниках скольжения, стремятся делать возможно тоньше (рис. 4)? В некоторых книгах утверждается, что эти меры способствуют уменьшению силы трения. |
 |
||||||||||
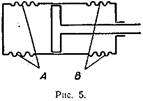
| 10. ИЗНОС СТЕНОК ЦИЛИНДРА ДВИГАТЕЛЯ ВНУТРЕННЕГО
СГОРАНИЯ. Внимательный осмотр достаточно долго прослужившего двигателя внутреннего сгорания показывает, что наибольший износ стенок его цилиндров сосредоточен в местах А и В, где происходит остановка и изменение направления движения поршня на противоположное (рис. 5). Казалось бы, этот факт противоречит «здравому смыслу», согласно которому износ должен быть особенно велик в тех местах, где скорость движения поршня максимальна. Ведь силы жидкого трения прямо пропорциональны величине скорости или даже (при больших скоростях) ее квадрату. В чем же дело? |
 |
||||||||||
| В начало Стр.2 | |||||||||||
|
2009 год |
|
||||||||||