
Электронный учебник по физике 10 класса
по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.
![]()
|
|
Электронный учебник по физике 10 класса по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.
|
|
|
Тесты по физике взяты из
сборника экзаменационных заданий физика ЕГЭ 2008 г. МЕХАНИКА А. Простые задания с вариантами ответов |
||||||||||
| Задание
1.1-А1. Поставлены две задачи: 1) рассчитать маневр стыковки двух космических кораблей; 2) рассчитать период обращения космических кораблей вокруг Земли. В каком случае космические корабли можно рассматривать как материальные точки? 1. Только в первом случае. 2. Только во втором случае. 3. В обоих случаях. 4. Ни в первом, ни во втором случае. Рекомендация по решению Задание 1.1-А2. Камень брошен из окна второго этажа с высоты 4 м и падает на землю на расстоянии 3 м от стены дома. Чему равен модуль перемещения камня? 1. 3 м. 2. 4 м. 3. 5 м. 4. 7 м. Рекомендации по решению |
|||||||||||
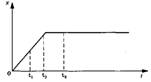
| Задание 1.1-АЗ. На рисунке представлен график зависимости координаты движущегося тела от времени. Сравните скорости v1, v2 и v3 тела в моменты времени t1, t2, t3. 1. v1>v2=v3 2. v1>v2>v3 3. v1<v2<v3 4. v1=v2>v3 Рекомендации по решению |
 |
||||||||||
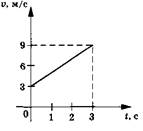
| Задание 1.1-А4.
По графику зависимости модуля скорости от времени, представленному на
рисунке, определите ускорение прямолинейного движения в момент времени
t = 2 с. 1. 2 м/с2. 2. 3м/с2. 3. 9 м/с2. 4. 27 м/с2. Рекомендации по решению |
 |
||||||||||
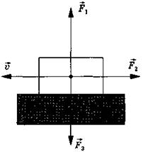
| Задание
1.1-А5.
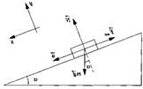
На рисунке показаны три равные по модулю силы, действующие на тело, и
его мгновенная скорость. Куда направлено ускорение тела? 1. Вверх. 2. Влево. 3. Вправо. 4. Направление ускорения по условию задачи определить нельзя. Рекомендации по решению |
 |
||||||||||
| Задание 1.1-А6.
Шарик, брошенный из точки А под углом к горизонту, проходит верхнюю
точку полета. Какая стрелка правильно указывает направление ускорения
тела, если сопротивлением воздуха можно пренебречь? 1. 1 2. 2 3. 3 4. 4 Рекомендации по решению |
|
||||||||||
| Задание 1.1-А7. Книга лежит на столе. На каком рисунке верно представлены силы взаимодействия книги и крышки стола? Рекомендации по решению |
 |
||||||||||
| Задание 1.1-А8.
Ученик провел опыты с двумя разными пружинами, измеряя силы упругости
при разных деформациях пружин. Результаты экспериментов приведены в
таблице. Закон Гука в условиях проведенных опытов... 1. ...подтверждается только для первой пружины. 2. ...подтверждается только для второй пружины. 3. ...подтверждается для обеих пружин. 4. ... не подтверждается ни для одной из пружин. Рекомендации по решению |
|
||||||||||
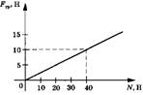
| Задание
1.1-А9.
На рисунке представлен график зависимости силы трения FTp
от модуля силы нормального давления N. Определить коэффициент трения
скольжения. 1. 0,1. 2. 0,2. 3. 0,25. 4. 0,5. Рекомендации по решению |
 |
||||||||||
| Задание
1.1-А10. В 1798 г. Генри Кавендиш провел измерение G-гравитационной
постоянной. Этот научный факт позволяет определить... 1. ...массу Земли. 2. ...период вращения Земли вокруг Солнца. 3. ...период вращения Земли вокруг своей оси. 4. ...расстояние от Земли до Солнца. Рекомендации по решению Задание 1.1-А11. Какое из приведенных ниже утверждений является определением, а какое - законом? 1. Импульс р равен произведению массы тела m на его скорость v . 2. Изменение импульса пропорционально силе F и времени t ее действия. 1. 1 — определение, 2 — закон. 2. 1 — закон, 2 — определение. 3. 1 и 2 — определения. Среди утверждений 1 и 2 нет ни определения, ни закона. Задание 1.1-А12. Тележка массой т, движущаяся со скоростью v, сталкивается с неподвижной тележкой такой же массы и сцепляется с ней. Скорость тележек после взаимодействия равна... 1. ...v/√2 2. ...v/2 3. ...v 4. ...2v Рекомендации по решению Задание 1.1-А13. Кинетическая энергия тела измеряется в тех же единицах, что и... 1. ...работа силы. 2. ...импульс силы. 3. ...мощность силы. 4. ...давление. Задание 1.1-А14. Кинетическая энергия тела равна 8 Дж, а величина импульса 4 Н*с. Масса тела равна... 1. ...0,5 кг. 2. ...1 кг. 3. ...2 кг. 4. ...32 кг. Рекомендации по решению Задание 1.1-А15. Подъемный кран поднимает вертикально вверх равномерно груз весом 1000 Н на высоту 5 м за 5 с. Какую механическую мощность развивает подъемный кран за время этого подъема? 1. 0 Вт. 2. 5000 Вт 3. 25 000 Вт. 4. 1000 Вт. Рекомендации по решению Задание 1.1-А16. Какое из значений для КПД наклонной плоскости, полученных учащимися при выполнении лабораторной работы, является заведомо неверным? 1. 1,5. 2. 0,75. 3. 0,60. 4. 0,33 Рекомендации по решению Задание 1.1-А17. Какие величины сохраняются для системы тел при упругом и неупругом ударах? 1. Суммарная механическая энергия и импульс шаров. 2. Только суммарная механическая энергия шаров. 3. Только суммарный импульс шаров. 4. Только суммарная скорость шаров. Рекомендации по решению Задание1.1-А18. Тормозной путь увеличивается при уменьшении... 1. ...угла наклона дороги к горизонту во время движения под гору. 2. ...коэффициента трения шин о дорогу. 3. ...скорости перед торможением. 4. ...массы автомобиля. Рекомендации по решению Задание 1.1-А19. Парашютист движется вертикально вниз с постоянной скоростью. При этом его... 1. ...потенциальная энергия превращается в кинетическую. 2. ...потенциальная энергия превращается во внутреннюю энергию системы «парашютист - воздух». 3. ...кинетическая энергия превращается в потенциальную. 4. ...кинетическая энергия превращается во внутреннюю энергию системы «парашютист - воздух». Рекомендации по решению Задание 1.1-А20. На рычаг действуют две перпендикулярные рычагу силы, плечи которых равны 0,1 м и 0,3 м. Сила, действующая на короткое плечо, равна 3 Н. Чему должна быть равна сила, действующая на длинное плечо, чтобы рычаг был в равновесии? 1. 1 Н. 2. 6 Н. 3. 9 Н. 4. 12 Н. Рекомендации по решению Задание 1.1-А21. Чему примерно равна архимедова сила, действующая на тело объемом 2 м3, наполовину погруженное в жидкость плотностью 1000 кг/м3? 1. 2000 Н. 2. 5000 Н. 3. 10 000 Н. 4. 20 000 Н. Рекомендации по решению |
|||||||||||
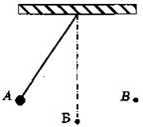
| Задание 1.1-А22.
Груз на нитке (см. рис.) начинает двигаться из точки А и далее совершает
колебания, проходя последовательно точки А-Б-В-Б-А и т. д. Период
колебания - это время его движения... 1. ...от точки А до точки Б. 2. ...от точки Б до точки В. 3. ...от точки А до точки В. 4. ...от точки А до точки В и обратно до точки А. |
 |
||||||||||
| Задание
1.1-А23. Тело колеблется вдоль оси х так, что его координата
меняется во времени по закону х = 5cos(πt) м. Период колебаний тела
равен... 1. ...0,5 с. 2. ...2 с. 3. ...л с. 4. ...5 с. Рекомендации по решению Задание 1.1-А24. Если массу груза уменьшить в 4 раза, то период колебаний груза на пружине... 1. ...увеличится в 4 раза. 2. ...увеличится в 2 раза. 3. ...уменьшится в 2 раза. 4. ...уменьшится в 4 раза. Рекомендации по решению Задание 1.1-А25. Вы услышали звуковой сигнал от источника, скрытого за препятствием. Этот факт можно объяснить, рассматривая звук как... 1. ...механическую волну. 2. ...поток частиц, вылетающих из источника звука. 3. ...поток молекул, составляющих воздух и движущихся от источника поступательно. 4. ...вихревой поток воздуха, идущий из источника звука. Задание 1.1-А26. Уравнение зависимости проекции скорости движущегося тела от времени: vx=2+3t(м/с). Каково соответствующее уравнение проекции перемещения тела? 1. rx = 2t + 3t2 (м). 2. rх = 1,5t2 (м). 3. rx = 2t + 1,5t2(м). 4. rx = 3t + t2 (м). Рекомендации по решению |
|||||||||||
| Задание
1.1-А27.
Специальный фотоаппарат зафиксировал два положения падающего в воздухе
из состояния покоя шарика: в начале движения и через 0,31с (см. рис.).
Ускорение свободного падения по результатам такого опыта приблизительно
равно... 1. ...10,0 м/с2. 2. ...10,5 м/с2. 3. ...9,2 м/с2. 4. ...11,0 м/с2. Рекомендации по решению |
 |
||||||||||
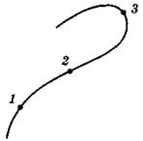
| Задание 1.1-А28.
Автомобиль движется с постоянной по модулю скоростью по траектории,
представленной на рисунке. В какой из указанных точек траектории
центростремительное ускорение максимально? 1. 1. 2. 2. 3. 3. 4. Во всех точках одинаково. Рекомендации по решению |
 |
||||||||||
| Задание
1.1-А29. Два школьника тянут динамометр в противоположные стороны,
прикладывая силы по 2 Н каждый. Чему равно показание неподвижного
динамометра? 1. 0 Н. 2. 4 Н. 3. 2 Н. 4. Ответ неоднозначен. Рекомендации по решению |
|||||||||||
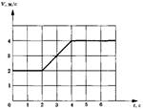
| Задание 1.1-АЗО.
Модуль скорости автомобиля массой 500 кг изменяется в соответствии с
графиком, приведенным на рисунке. Определите модуль равнодействующей
силы в момент времени t = 3 с. 1. 0 Н. 2. 500 Н. 3. 1000 Н. 4. 2000 Н. Рекомендации по решению |
 |
||||||||||
| РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТЕСТОВЫХ ЗАДАНИЙ | |||||||||||
| Задание 1.1-А1. Воспользоваться определением материальной точки - тело, размерами которого можно пренебречь по сравнению с другими размерами в данной задаче. К задаче | |||||||||||
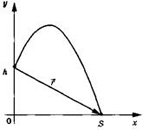
| Задание 1.1-А2.
Сделать рисунок. Использовать определение вектора перемещения -это
вектор, соединяющий начальное и конечное положение тела. Воспользоваться
теоремой Пифагора для сторон прямоугольного треугольника: r2
= h2
+ S2.
К задаче |
 |
||||||||||
|
Задание 1.1-A3. На графике зависимости
координаты тела от времени проекция вектора скорости в данный момент
времени численно равна тангенсу угла наклона графика (чем «круче» к оси
абсцисс расположен график, тем проекция скорости больше; проекция
скорости равна нулю, если график расположен параллельно оси времени,
координата при этом не меняется — тело покоится).
К задаче
Задание 1.1-А4. При прямолинейном равноускоренном движении (из графика видно, что скорость тела увеличивается) модуль ускорения равен отношению изменения скорости к промежутку времени, за которое это изменение произошло:a=Δv/Δt. По графику определяют, что, например, за промежуток времени 3 с (от 0 до 3 с) модуль скорости увеличился с 3 до 9 м/с, т. е. на 6 м/с. К задаче Задание 1.1-А5. Воспользоваться вторым законом Ньютона: ускорение тела прямо пропорционально действующей на него равнодействующей силе и обратно пропорционально массе тела. Равнодействующая сила — векторная сумма всех сил, действующих на тело. К задаче Задание 1.1-А6. При отсутствии сопротивления воздуха на шарик действует только сила тяжести, направленная вниз. Далее надо применить второй закон Ньютона. К задаче Задание 1.1-А7. Применить третий закон Ньютона: силы взаимодействия двух тел равны по модулю, противоположны по направлению, приложены к взаимодействующим телам и направлены вдоль одной прямой. К задаче Задание 1.1-А8. Воспользоваться законом Гука: модуль силы упругости Fynp прямо пропорционален деформации х пружины Fynp = kx, где k — коэффициент пропорциональности. К задаче Задание 1.1-А9. Применить закон для модуля силы трения скольжения FTp: FTp = μN, где μ — коэффициент трения; N — модуль силы нормальной реакции опоры. По приведенному графику определить, что, например, при N = 40 Н и FTP = 10 Н. К задаче Задание 1.1-А10. Использовать закон всемирного тяготения для модуля силы F взаимодействия Земли массой М3 с телом массой т, расположенным на ее поверхности: F =GMз*m/R2з , где R3 — радиус Земли. К задаче Задание 1.1-А12. Применить закон сохранения импульса системы тел в проекции на координатную ось, направленную вдоль направления движения тележки: m1v1 + m2v2 = (т1 + т2)и, где т1 = т — масса движущейся тележки; v1=v — ее скорость; т2 = т — масса неподвижной тележки; v2 = 0 — ее скорость; и — скорость тележек после их взаимодействия (абсолютно неупругого удара). К задаче Задание 1.1-А14. Воспользоваться формулами кинетической энергии тела Ek=mv2/2 и модулем (величиной) импульса р = mv, и решить полученную систему уравнений относительно искомой величины m. К задаче Задание 1.1-А15. При равномерном подъеме груза поднимающая сила равна по модулю силе тяжести, которая равна по модулю весу груза: F = Р = 1000 Н. Работа поднимающей силы равна А = FScosa = Ph, где S = h = 5 м — высота подъема груза; а = 0 — угол между направлением поднимающей силы и направлением перемещения груза. Мощность крана равна N=A/t, где t = 5 с — время подъема груза. К задаче Задание 1.1-А16. КПД не может быть больше 100% = 1. К задаче Задание 1.1-А17. При любом ударе (как упругом, так и не упругом) сохраняется импульс системы. К задаче |
|||||||||||
|
Задание 1.1-А18.
При движении по наклонной поверхности под гору модуль силы трения равен
FTP
=μN = μmgcosa, где N — модуль силы нормальной реакции опоры; тg — модуль
силы тяжести; g — величина ускорения свободного падения; a — угол,
который составляет наклонная плоскость с горизонтом. Модуль ускорения а
автомобиля при равнозамедленном движении можно найти из второго закона
Ньютона в проекции на ось, направленную вдоль наклонной плоскости вверх:
а =(Fтр-mgsina)/m = g(μcosa-sina), где т —масса автомобиля. С другой
стороны, при равнозамедленном движении модуль ускорения а, пройденный до
остановки путь S и модуль v0 вектора начальной скорости связаны
соотношением: 2aS = v20 . Решая полученную систему уравнений, можно получить: S =v20/(2g(μcosa-sina) . Из последней формулы видно, что тормозной путь не зависит от массы тела, уменьшается при уменьшении скорости перед торможением и увеличивается при уменьшении коэффициента трения шин о дорогу. К задаче |
 |
||||||||||
| Задание
1.1-А19. При движении парашютиста вертикально вниз с постоянной
скоростью его кинетическая энергия не изменяется, а потенциальная
энергия уменьшается. При этом она превращается во внутреннюю энергию
системы «парашютист - воздух». К задаче
Задание 1.1-А20. Воспользоваться уравнением равновесия рычага: М1 = М2, где М1 — момент первой силы, а М2 — момент второй силы. Воспользоваться определением момента силы: М = Fl, где F — модуль силы; l — плечо силы. К задаче Задание 1.1-А21. Применить формулу для расчета архимедовой (выталкивающей) силы: Fa = pgVпогр, где ρ=1000 кг/м2 — плотность жидкости; g = 10 м/с2 — модуль ускорения свободного падения; Vпогр =0,5V= — объем тела, погруженного в жидкость К задаче Задание 1.1-А23. Воспользоваться формулой координаты при гармонических колебаний: X = Acos(ωt + φ0), где А — амплитуда колебаний; ω — циклическая частота колебаний; φ0 — начальная фаза. Путем сравнения с законом, заданным в условии задачи, определить величину ω =π рад/с. Применить формулу, связывающую циклическую частоту и период колебаний: Т=2π/ω К задаче Задание 1.1-А24. Применить формулу для периода колебаний пружинного маятника: Т = 2π√(m/k)—, где m — масса груза; k — жесткость пружины. К задаче Задание 1.1-А26. Написать уравнение проекции скорости при равнопеременном движении vx = vох + axt, где vох — проекция начальной скорости; ах — проекция ускорения. Путем сравнения с формулой проекции скорости, заданной в условии задания, получаем vox = 2 м/с, ах = 3 м/с2. Написать общее уравнение проекции перемещения и подставить полученные числовые значения: r=voxt+axt2/2=2t+1,5t2(м). К задаче Задание 1.1-А27. Из рисунка определить, что шарик пролетает расстояние h = 44 см = 0,44 м. Применить формулу пройденного пути при свободном падении тела: h =gt2/2, где t = 0,31 с — время свободного падения тела. К задаче Задание 1.1-А28. Применить формулу для модуля центростремительного ускорения при движении тела по криволинейной траектории: ацс =v2/2, где v — модуль вектора скорости; R — радиус кривизны траектории в данной точке. Так как модуль скорости точки постоянен, то центростремительное ускорение максимально в точке, в которой радиус кривизны траектории минимален. К задаче Задание 1.1-А29. Если к пружине динамометра и к его корпусу приложить равные по модулю и противоположные по направлению силы, то он останется в положении равновесия, и показание динамометра будет равно модулю приложенных сил. К задаче Задание 1.1-А30. По графику определить, что для участка графика, содержащего момент времени t = 3 с, за промежуток времени Δt = 4-2 = 2с изменение скорости равно Δv = 4 - 2 = 2 м/с. Рассчитать величину ускорения по формуле а = Δv/Δt. Определить модуль равнодействующей силы по второму закону Ньютона: F = та, где т = 500 кг — масса тела. К задаче |
|||||||||||
|
В начало
|
|||||||||||
|
2009 год |
|
||||||||||