
Электронный учебник по физике 10 класса
по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.
![]()
|
|
Электронный учебник по физике 10 класса по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.
|
|
|
Тесты по физике взяты из
сборника экзаменационных заданий физика ЕГЭ 2008 г. МЕХАНИКА В. Задания повышенного уровня сложности |
||||||||||
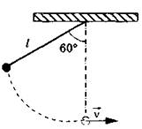
| Задание 1.1-В1. Груз массой т = 0,2 кг привязан к нити длиной 1 = 1 м. Нить с грузом отвели на угол 60° (см. рис.). Чему равна кинетическая энергия груза при прохождении им положения равновесия? Полученный ответ округлить до целых Рекомендации по решению |
 |
||||||||||
| Задание 1.1-В2.
Тело массой 1 кг бросили с поверхности Земли со скоростью 20 м/с под
углом 45° к горизонту. Чему равна работа силы тяжести за время полета тела (от
броска до падения на Землю)? Сопротивлением воздуха пренебречь.
Рекомендации по решению Задание 1.1-ВЗ. Сани с седоками общей массой 100 кг съезжают с горы высотой 8 м и длиной 100 м. Какова средняя сила сопротивления движению санок, если в конце горы они достигли скорости 10 м/с, а начальная скорость равна нулю? Рекомендации по решению Задание 1.1-В4. Груз массой 0,1 кг привязали к нити длиной 1 м. Нить отвели от вертикали на угол 90°, и груз отпустили. Каково центростремительное ускорение груза в момент, когда нить образует с вертикалью угол 60°? Сопротивлением воздуха пренебречь. Рекомендации по решению Задание 1.1-В5. Тело массой 0,1 кг колеблется так, что проекция ах ускорения его движения зависит от времени в соответствии с уравнением ах = 10sin(2πt/10) . Чему равна проекция силы на ось ох, действующей на тело в момент времени t =5/6 с? Умножьте ответ на 10. Рекомендации по решению |
|||||||||||
| С. Задания, требующие развернутого ответа | |||||||||||
| Задание
1.1-С1. Два тела массой М подвешены на невесомом блоке при помощи
легкой нити и находятся в равновесии. К одному из них подвесили груз
массой 2М, и система пришла в движение. С какой силой груз массой 2М
действует на нить, соединяющую грузы массами М и 2М?
Рекомендации по решению Задание 1.1-С2. На одном конце тележки длиной l = 5м стоит человек массой т = 40 м. Масса тележки М = 60 кг. На какое расстояние относительно пола передвинется тележка, если человек перейдет с постоянной скоростью на другой ее конец? Массой колес и трением пренебречь. Рекомендации по решению Задание 1.1-СЗ. Тяжелый мячик отпустили без начальной скорости с высоты Н = 20 м, при ударе о землю он потерял часть своей кинетической энергии и долетел до верхней точки через t = 3 с после начала движения. Какая часть кинетической энергии перешла в тепло при ударе? Сопротивлением воздуха пренебречь. Рекомендации по решению |
|||||||||||
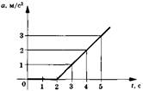
| Задание 1.1-С4. К покоящемуся на шероховатой поверхности телу приложена сила тяги F =bt, где b— постоянная величина. На рисунке представлен график зависимости ускорения тела от времени. Определить коэффициент трения скольжения. Рекомендации по решению |
 |
||||||||||
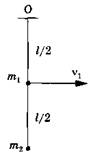
| Задание 1.1-С5. Точечные массы т1 = 0,25 кг и т2 = 0,5 кг прикреплены к невесомому стержню длиной l— 1 м, как показано на рисунке. Стержень вращается вокруг горизонтальной оси, проходящей через точку O. В какой-то момент времени груз массой т1 имеет скорость v1 = 1 м/с. Определить силу, с которой стержень действует на массу т2 в этот момент времени. Рекомендации по решению |
 |
||||||||||
| РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ТЕСТОВЫХ ЗАДАНИЙ | |||||||||||
|
В. Задания повышенного уровня сложности Задание 1.1-В1. Воспользоваться законом сохранения механической энергии (сопротивлением воздуха пренебрегаем, а сила натяжения нити работы не совершает, так как в каждый момент времени во время движения направлена перпендикулярно вектору скорости): Еп1 = Ек2, где Еп1 — потенциальная энергия груза в верхнем (первом) положении; Ек2 — кинетическая энергия груза в нижнем (втором) положении. Учтено, что в верхнем положении скорость груза равна нулю, а за нулевой уровень отсчета потенциальной энергии груза в поле силы тяжести Земли принят уровень груза в нижнем положении. Тогда Еп2 = mgh = mg(l-lcosa) = mgl(1 - cosa), где h — разница высот груза в верхнем и нижнем положениях. К задаче Задание 1.1-В2. Воспользоваться свойством потенциальных сил, работа которых не зависит от формы траектории, а зависит только от начального и конечного положений тела. В качестве траектории взять соединяющий начальное и конечное положения отрезок прямой, расположенной параллельно поверхности Земли. Тогда работа сила тяжести равна А = mgScosa, где mg — модуль силы тяжести; S — дальность полета тела; a — угол между вертикально направленной силой тяжести и горизонтальным направлением вектора перемещения тела. Поскольку a = 90°, то А = 0 К задаче Задание 1.1-ВЗ. Применить закон изменения механической энергии: ΔЕ = Е2- Е1 = AFc. Е1 = mgh — механическая энергия саней в первом (верхнем) состоянии, когда их скорость и, следовательно, кинетическая энергия равна нулю, т = 100 кг — масса саней, h = 8 м — высота горы. Е2 =mv2/2
механическая энергия саней во втором (нижнем) состоянии, где v = 10 м/с
— скорость саней в этом состоянии. Работа силы сопротивления при спуске
саней с горы рассчитывается по формуле:
AFc
= FcScosa, где Fc — искомая
сила сопротивления движению санок; S = 100 м — длина горы; a=180° — угол
между направлением силы сопротивления и направлением вектора перемещения
саней. К задаче |
|||||||||||
| Задание 1.1-В5. Применить второй закон Ньютона для определения проекции силы: Fx = max, где m = 0,1 кг — масса тела. К задаче | |||||||||||
| С. Задания,
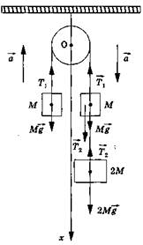
требующие развернутого ответа Задание 1.1-С1. Записать уравнения движения грузов в проекции на направленную вертикально вниз координатную ось, при этом учесть, что модули ускорений a грузов равны, равны по модулю силы натяжений нитей T1 между грузами массами М и силы натяжений нитей Т2 между грузами массами М и 2М. Для груза массой 2М: 2Mg - Т2 = 2Ма; для движущегося вниз груза массой М: Mg + Т2 - Т1 = Ма; для движущегося вверх груза массой М: Mg - Т1 = -Ма. Решая полученную систему уравнений, можно определить искомую величину Т2 К задаче |
 |
||||||||||
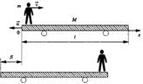
| Задание 1.1-С2. При движении человека относительно тележки со скоростью v тележка (вместе с человеком) движется в противоположную сторону со скоростью u . Применить классический закон сложения скоростей: скорость человека относительно земли равна: v1=v+u, а её модуль v1=v-u. Использовать закон сохранения импульса системы человек — тележка в системе отсчета, связанной с землей (применять закон можно, так как трения нет): m*v1+M*u=0. В уравнении справа стоит ноль, так как тележка покоится, если человек неподвижен. Записать закон в проекции на ось, направленную вдоль вектора скорости человека относительно тележки: m(v - u) - М*u = 0. Решить полученное уравнение относительно величины и =m*v/(M+m). Определить время движения человека по тележке: t =l/v . Найти искомую величину перемещения тележки: S = ut =m*v/(M+m)*l/v=m*l/(M+m). К задаче |
 |
||||||||||
|
Задание 1.1-СЗ. Определить механическую
энергию мячика в начальной точке, которая равна его потенциальной
энергии (так как скорость мячика в верхней точке равна нулю): Е1
= Еп1
= mgH. Такой же механической, но уже кинетической, энергией обладает мяч
перед ударом о землю, так как сопротивлением воздуха пренебрегаем. Найти
время свободного падения мяча по формуле:
Н=(gt22 )/2,
откуда t1= √(2H/g)=√(2*20/10)=2 с . Определить время движения мяча
вверх:
t2=
t-t1= 3-2=1с и высоту
подъема мяча после удара h =gt22/2.
Рассчитать механическую (потенциальную) энергию мяча на высоте h: Е2=Еп2=mgh.
Такой же механической (кинетической) энергией обладает мяч после удара о
землю. Написать закон превращения части механической энергии в тепловую
энергию Q при ударе о землю: Е1+Е2+Q
и определить величину Q. Рассчитать, какая часть механической
(кинетической) энергии перешла в тепло при ударе: Q/E1.
К задаче ацс=v22/l=2v1/l=4v12/l . Решить первое уравнение относительно величины Т К задаче |
|||||||||||
|
С1 Тело, свободно падающее с некоторой высоты без начальной скорости, за время τ = 1 с после начала движения проходит путь в п = 5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения. Ответ: t=3c С1 Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна 1 м/с. Ответ: L=0,173 м |
|||||||||||
|
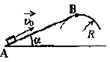
С1 Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рисунок). В точке касания В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R = 0,4 м. Если в точке А скорость шайбы превосходит v0= 4 м/с, то в точке В шайба отрывается от опоры. Длина наклонной плоскости АВ = L=1 м, угол а = 30°. Найдите коэффициент трения μ между наклонной плоскостью и шайбой. Ответ 0,15 |
 |
||||||||||
|
C1 Вертикально расположенный замкнутый цилиндрический сосуд высотой 50 см разделен подвижным поршнем весом 110 Н на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 К. Сколько молей газа находится в каждой части цилиндра, если поршень находится на высоте 20 см от дна сосуда. Толщиной поршня пренебречь. Ответ: 0,022 моль |
 |
||||||||||
|
С1 В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз и нагрели на 60 К. При этом объем, занимаемый воздухом, не изменился. Давление атмосферы в лаборатории-750 мм рт.ст. Какова температура воздуха в лаборатории? Ответ: T0=300К |
|||||||||||
|
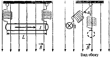
C3 По прямому горизонтальному проводнику длиной 1 м с площадью поперечного сечения 1,25*10-5м2 подвешенному с помощью двух одинаковых невесомых пружинок жесткостью 100 Н/м, течет ток I= 10 А (см. рисунок). Какой угол а составляют оси пружинок с вертикалью при включении вертикального магнитного поля с индукцией В= 0,1 Тл, если абсолютное удлинение каждой из пружинок при этом составляет 7*10-3 м? (Плотность материала проводника 8*103 кг/м3). Ответ: a=45 |
 |
||||||||||
|
C3 Положительно заряженная пылинка, имеющая массу 10-8 г и заряд 1,8*10-14 Кл, влетает в электрическое поле конденсатора в точке, находящейся посередине между его пластинами (см. рисунок). Минимальная скорость, с которой пылинка должна влететь в конденсатор, чтобы затем пролететь его насквозь, равна 30 м/с. Расстояние между пластинами конденсатора 1 см, напряженность электрического поля внутри конденсатора 500 кВ/м. Чему равна длина пластин конденсатора? Силой тяжести пренебречь. Система находится в вакууме. Ответ: l=0,1м. |
|||||||||||
|
С4 Условимся считать изображение на пленке фотоаппарата резким, если вместо идеального изображения в виде точки на пленке получается изображение пятна диаметром не более некоторого предельного значения. Поэтому, если объектив находится на фокусном расстоянии от пленки, то резкими считаются не только бесконечно удаленные предметы, но и все предметы, находящиеся дальше некоторого расстояния d. Оцените предельный размер пятна, если при фокусном расстоянии объектива 50 мм и диаметре входного отверстия 5 мм резкими оказались все предметы, находившиеся на расстояниях более 5 м от объектива. Сделайте рисунок, поясняющий образование пятна. Ответ: =0,05м. |
|||||||||||
|
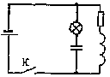
С4 В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В; емкость конденсатора 2 мФ; индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом. В начальный момент времени ключ K замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока пренебречь. Сопротивлением катушки и проводов пренебречь. Ответ: =0,115Дж. |
 |
||||||||||
|
В начало
|
|||||||||||
|
2009 год |
|
||||||||||