Лабораторные работы

Электронный учебник по физике 10 класса

по учебнику Мякишева Г.Я., Буховцева Б.Б., Сотского Н.Н.

Лабораторные работы по физике

Типовая инструкция по правилам безопасности труда для учащихся

1. Будьте внимательны и дисциплинированны, точно выполняйте указания учителя.

2. Не приступайте к выполнению работы без разрешения учителя.

3. Размещайте приборы, материалы, оборудование на своем рабочем месте таким образом, чтобы исключить их падение или опрокидывание.

4. Перед выполнением работы внимательно изучите ее содержание и ход выполнения.

5. Для предотвращения падения стеклянные сосуды (пробирки, колбы) при проведении опытов осторожно закрепляйте в лапке штатива.

6. При проведении опытов не допускайте предельных нагрузок измерительных приборов. При работе с приборами из стекла соблюдайте особую осторожность. Не вынимайте термометры из пробирок с затвердевшим веществом.

7. Следите за исправностью всех креплений в приборах и приспособлениях. Не прикасайтесь и не наклоняйтесь (особенно с неубранными волосами) к вращающимся частям машин.

8. При сборке экспериментальных установок используйте провода (с наконечниками и предохранительными чехлами) с прочной изоляцией без видимых повреждений.

9. При сборке электрической цепи избегайте пересечения проводов. Запрещается пользоваться проводником с изношенной изоляцией и выключателем открытого типа (при напряжении выше 42 В).

10. Источник тока к электрической цепи подключайте в последнюю очередь. Собранную цепь включайте только после проверки и с разрешения учителя. Наличие напряжения в цепи можно проверять только с помощью приборов или указателей напряжения.

11. Не прикасайтесь к находящимся под напряжением элементам цепей, лишенным изоляции. Не производите пересоединения в цепях и смену предохранителей до отключения источника электропитания.

12. Следите за тем, чтобы во время работы случайно не коснуться вращающихся частей электрических машин. Не производите пересоединения в электрических цепях машин до полной остановки якоря или ротора машины.

Оценка лабораторных и практических работ

Оценка «5» ставится в том случае, если учащийся:
а) выполнил работу в полном объеме с соблюдением необходимой последовательности проведения опытов и измерений;
б) самостоятельно и рационально выбрал и подготовил для опыта необходимое оборудование, все опыты провел в условиях и режимах, обеспечивающих получение результатов и выводов с наибольшей точностью;
в) в представленном отчете правильно и аккуратно выполнил все записи, таблицы, рисунки, чертежи, графики, вычисления и сделал выводы;
г) правильно выполнил анализ погрешностей (VIII—X классы);
д) соблюдал требования безопасности труда.
Оценка «4» ставится в том случае, если выполнены требования к оценке «5», но:
а) опыт проводился в условиях, не обеспечивающих достаточной точности измерении,
б) или было допущено два-три недочета, или не более одной негрубой ошибки и одного недочета.
Оценка «3» ставится, если работа выполнена не полностью, но объем выполненной части таков, что позволяет получить правильные результаты и выводы, или если в ходе проведения опыта и измерений были допущены следующие ошибки:
а) опыт проводился в нерациональных условиях, что привело к получению результатов с большей погрешностью,
б), или в отчете были допущены в общей сложности не более двух ошибок (в записях единиц, измерениях, в вычислениях, графиках, таблицах, схемах, анализе погрешностей и т. д.), не принципиального для данной работы характера, но повлиявших на результат выполнения,
в) или не выполнен совсем или выполнен неверно анализ погрешностей (VIII—X класс);
г) или работа выполнена не полностью, однако объем выполненной части таков, что позволяет получить правильные результаты и выводы по основным, принципиально важным задачам работы.
Оценка «2» ставится в том случае, если:
а) работа выполнена не полностью, и объем выполненной части работы не позволяет сделать правильных выводов,
б) или опыты, измерения, вычисления, наблюдения производились неправильно,
в) или в ходе работы и в отчете обнаружились в совокупности все недостатки, отмеченные в требованиях к, оценке «3».
Оценка «1» ставится в тех случаях, когда учащийся совсем не выполнил работу или не соблюдал требований безопасности труда.

В тех случаях, когда учащийся показал оригинальный и наиболее рациональный подход к выполнению работы и в процессе работы, но не избежал тех или иных недостатков, оценка за выполнение работы по усмотрению учителя может быть повышена по сравнению с указанными выше нормами.

Введение

Все, что сказано в этом введении, запоминать не нужно. Это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значений физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины но формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

А, В, С, ... — физические величины.

Апр — приближенное значение физической величины, т. е. значение, полученное путем прямых или косвенных измерений.

ΔА — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

ε= ΔА/ Апр *100%

ΔАи— абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; см. табл. 1.

ΔАо— абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене делении секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной
погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔА=ΔАи+ΔАо

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (А = 0,17≈0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А= 10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае Апр находят как среднее арифметическое значение всех измерений, а ΔА (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Абсолютные инструментальные погрешности средств измерений Таблица 1.

№ п/п	Средства измерений	Предел измерений	Цена деления	Абсолютная инструментальная погрешность
1	Линейка ученическая чертёжная инструментальная (стальная) демонстрационная	До 50 см До 50 см 20 см 100 см	1мм 1мм 1мм 1см	±1мм ±0,2мм ±0.1мм ±0.5см
2	Лента измерительная	150 см	0,5 см	±0,5 см
3	Измерительный цилиндр	До 250 мм	1 мл	±1 мл
4	Штангенциркуль	150 мм	0,1 мм	±0,05 мм
5	Микрометр	25 мм	0,01 мм	±0,005 мм
6	Динамометр учебный	4 Н	0,1	±0,05 Н
7	Весы учебные	200 г	—	±0,01 г
8	Секундомер	0—30 мин	0,2 с	±1 с за 30 мин
9	Барометр-анероид	720-780 мм	1 ммрт. ст.	±3 мм рт. ст.
10	Термометр лабораторный	0—100 °С	1 °С	±1°С
11	Амперметр школьный	2 А	0,1 А	±0,05 А
12	Вольтметр школьный	6 В	0,2 В	±0,15 В

Относительная погрешность косвенных измерений определяется так, как показано в таблице 2.

№ п/п	Формула физической величины	Формула относительной погрешности
1	A=BCD A=B/(CD)	ε= ΔB/B+ΔC/C+ΔD/D
2	A=B+C	ε= (ΔB+ΔC)/(B+C)
3	A=B(C/D)	ε =ΔB/B+1/2ΔC/C+1/2ΔD/D

Абсолютная погрешность косвенных измерений определяется по формуле ΔА=Апрε (ε выражается десятичной дробью).

2. О классе точности электроизмерительных приборов
Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ np измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность ΔAи от всей шкалы прибора (Аmax): γnp = (ΔAи/ Аmax )*100%
Класс точности указывают на шкале прибора или в его паспорте (знак % при этом не пишется). Существуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ np) и всю его шкалу (Аmax), определяют абсолютную погрешность ΔAи измерения физической величины А этим прибором: ΔAи= γnp Аmax/100

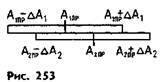
3. Как сравнивать результаты измерений
1. Записать результаты измерений в виде двойных неравенств:
A1пр – ΔА1< A1пр < A1пр+ ΔА1
A2пр-ΔА2 < A2пр < A2пр+ ΔА2
Сравнить полученные интервалы значений (рис. 253): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений

4. Как оформлять отчет о проделанной работе
1. Лабораторная работа № ... .
2. Наименование работы.
3. Цель работы.
4. Чертеж (если требуется).
5. Формулы искомых величин и их погрешностей.
6. Таблица с результатами измерений и вычислений.
7. Окончательный результат, вывод и пр. (согласно цели работы).

5. Как записывать результат измерения
А=Aпр ± ΔA
ε = ...%.

Приближенные вычисления без точного учёта погрешностей.

1°. Производя обработку многочисленных измерений, часто не подсчитывают погрешности отдельных результатов и судят о погрешности приближенного значения величины (числа), указывая количество верных значащих цифр в этом числе.

Нули, стоящие в числе слева, значащими цифрами не считаются. Нули в середине или в конце числа (справа), обозначающие отсутствие в числе единиц соответствующих разрядов,— значащие цифры. Например, в числе 0,08040 первые два нуля — незначащие, а третий и четвертый — значащие.

Нули, поставленные в конце целого числа взамен неизвестных цифр и служащие лишь для определения разрядов остальных цифр, значащими не считаются. В подобных случаях нули в конце числа лучше не писать и заменять их соответствующей степенью числа 10. Например, если число 4200 измерено с абсолютной погрешностью ±100, то это число должно быть записано в виде 42*10² или 4,2*10³. Такая запись подчеркивает, что в данном числе содержатся лишь две значащие цифры.

2°. Если приближенное значение величины содержит лишние или недостоверные цифры, то его округляют, сохраняя только верные значащие цифры и отбрасывая лишние. При этом руководствуются следующими правшами округления:

а) Если первая отбрасываемая цифра больше 4, то последняя сохраняемая цифра увеличивается на единицу. Например, округляя число 27,3763 до сотых, следует записать 27,38.

б) Если первая отбрасываемая цифра меньше 4 или равна 4, то последняя сохраняемая цифра не изменяется. Например, округляя число 13 847 до сотен, записывают 138*10².

в) Если отбрасываемая часть числа состоит из одной цифры 5, то число округляют так, чтобы последняя сохраняемая цифра была четной. Например, при округлении до десятых 23,65≈23,6, но 17,75≈ 17,8.

3°. Производя различные математические действия с приближенными числами, руководствуются следующими правилами подсчета цифр:

а) При сложении и вычитании в результате сохраняют столько десятичных знаков, сколько их содержится в числе с наименьшим количеством десятичных знаков.

б) При умножении и делении в результате сохраняют столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр.

Исключения из этого правила допускаются в тех случаях, когда один из сомножителей произведения начинается с единицы, а сомножитель, содержащий наименьшее количество значащих цифр,— с какой-нибудь другой цифры. В этих случаях в результате сохраняют на одну цифру больше, чем в числе с наименьшим количеством значащих цифр.
в) Результат расчета значений функций xⁿ, и lgx некоторoгo приближенного числа х должен содержать столько значащих цифр, сколько их имеется в числе x. При вычислении промежуточных результатов сохраняют на одну цифру больше, чем рекомендуют правила а) — в) (так называемая запасная цифра). В окончательном результате запасная цифра отбрасывается.

Если некоторые приближенные числа содержат больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня и т. д.), чем другие, то их предварительно округляют, сохраняя только одну лишнюю цифру.

Пример I. Перед сложением приближенных чисел 0,374; 13,1 и 2,065 первое и третье из них нужно округлить до сотых, а в окончательном результате сотые отбросить: 13,1+2,06 + 0,37 ≈15,5.

Пример 2. Результат расчета выражения дол(жен содержать только две значащие цифры (по количеству значащих цифр в числе 7,2):

Пример 3. Результат перемножения чисел 13,27 и 0,84 можно записать с тремя значащими цифрами (см. исключение из правила б)):

13,27-0,84≈ 13,3*0,84 ≈11,2 (а не 11),

Пример 4. При возведении в куб приближенного числа 216 результат должен быть записан только с тремя значащими цифрами: 216³≈ 101*10⁵.

В начало

2009 год

Сайт управляется системой uCoz